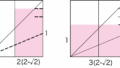
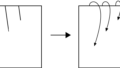
三角形の2等分線を使うと、2本の辺の比率で折り出しができます。多角形の作図などでは活用されていますが、いわゆる比の折り出しではあまり使われていないようです。
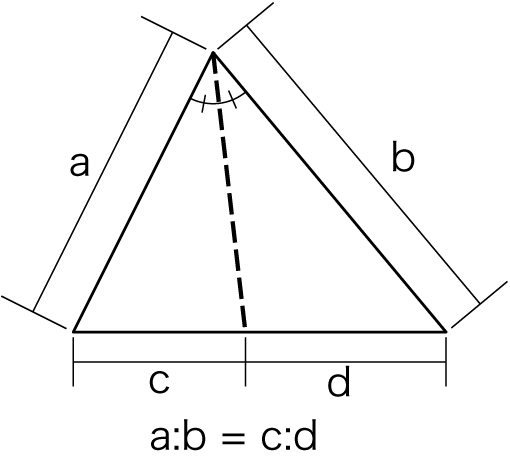
例として、3:4:5の直角三角形を見てみます。まず、4+5=9等分の方法。三角形の位置を変えて、等分する三角形の辺を正方形の辺と合わせているのが、実用性に関するポイントです。
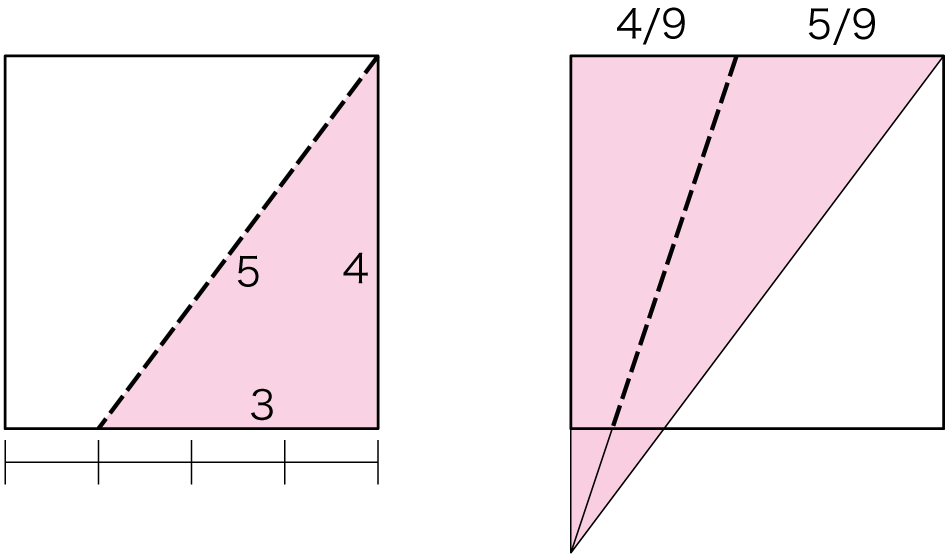
違う方向に折ると3+5=8等分ができます。しかしこれは残念ながらあまり嬉しくない。またもう一つ、直角のカドの2等分線で、3+4=7等分も可能です。これは結果的に2本の対角線を交差させる方法と同じ結果となっています。
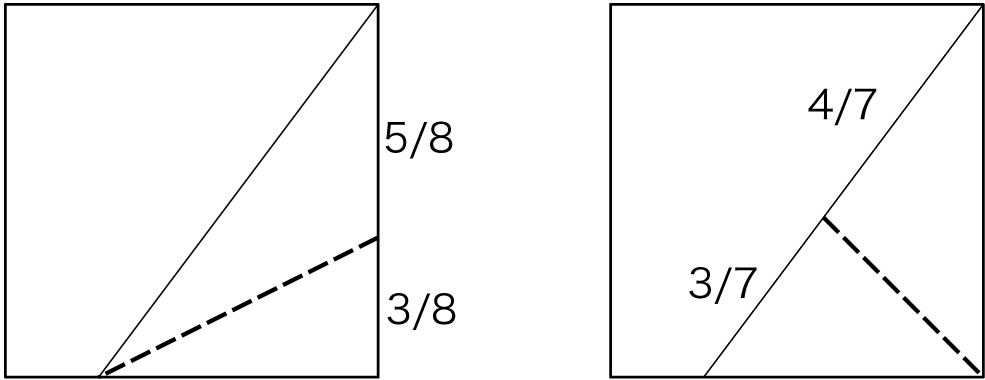
実用面から考えると、欲しい数字を持つ三角形をどのようにして折り出すかがポイントとなります。また、正方形(もしくは長方形)から折り出すことを考えると、直角三角形が扱いやすいでしょう。というか、それ以外だと結構面倒。
各辺が整数の直角三角形、ピタゴラスの三角形は、わかりやすい使い方になります。結構いろいろな数値を折り出すことができます。5:12:13から、17等分、18等分、25等分。8:15:17からは、23等分、25等分、そして32等分が可能です。
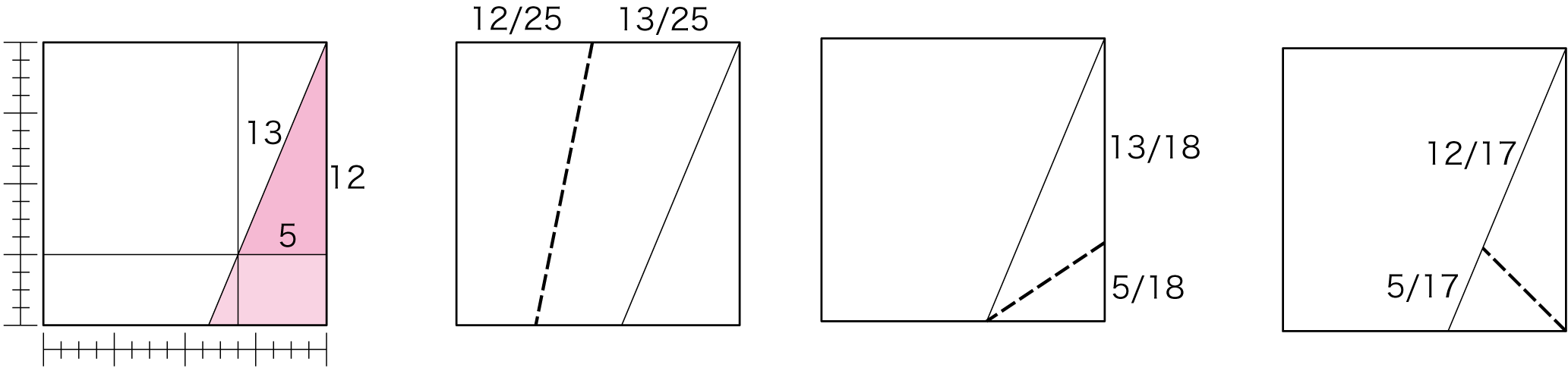
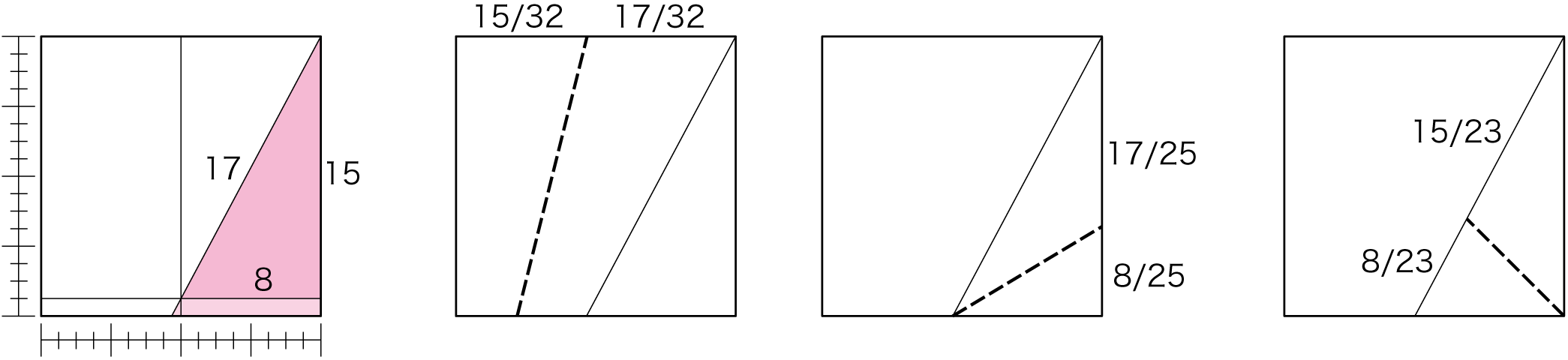
それ以外では、必要な比率を持つ三角形を用意する必要があります。例として、2+3=5等分を考えてみました。手順は以下のようなりますが、仕組みを知らないと理解が難しそう。なお、√5が降り出せるので、これを使った比の折り出しもできます。3+√5など、使い所がすぐに思いつかないが面白い比率です。
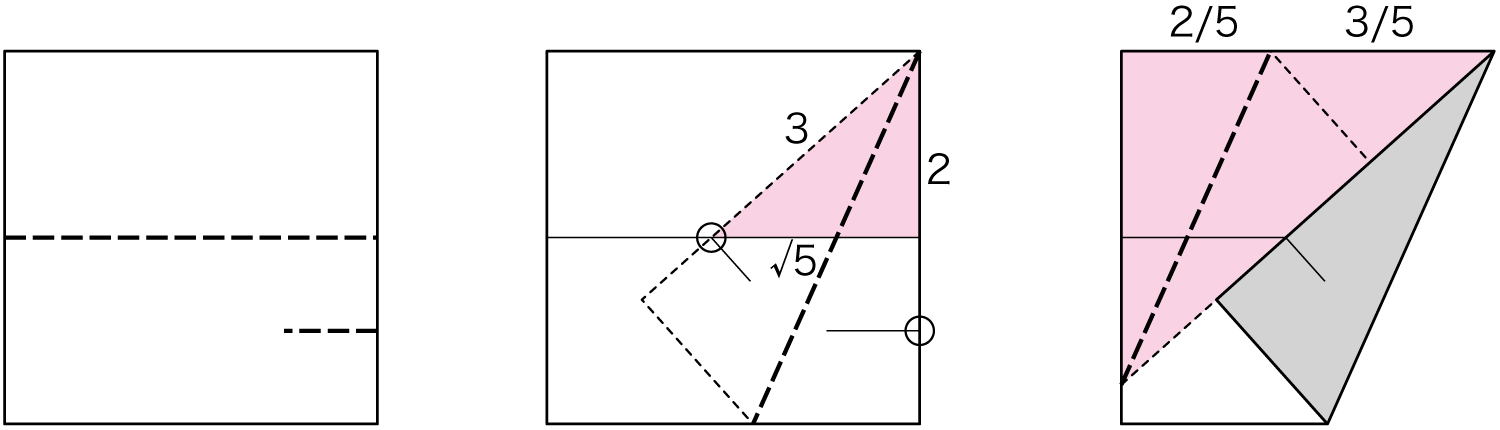
ということで、整数以外にも、たとえば√3や√5などは、直角三角形の辺として折り出しやすいので普通に使えます。特に√5は実際に黄金比の折り出しによく活用されています。
他、ちょっと面白い例としては、30°を使った折り出し方法は、この方法と考えることもできます。
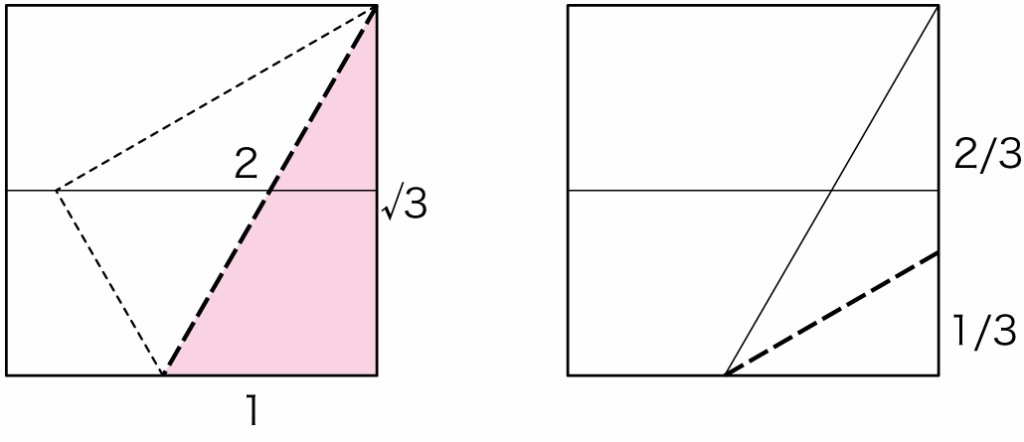
以上、使える数字に条件はあるものの、うまく使えばいろいろな比率を折り出すことができそうです。