韓国コンベンションに参加した際に、この比率を使用している作品について話題になり、折り出しを考えてみました。
まず、基本的な事として、2つの対角線を交差させる折り出し方法では、「2つの折り出しやすい数字に分ける」のが重要です。今回の場合、いくつかの候補から、「12-6√2:-1」に分けるのがよさそうだと考えました。
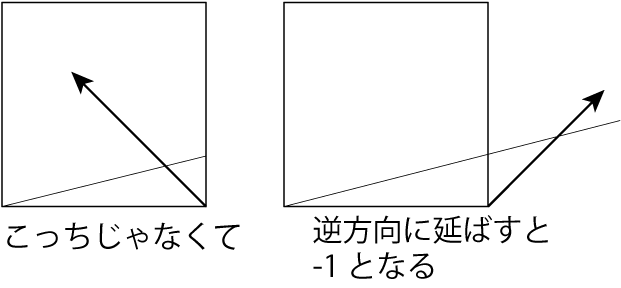
……「-1」ってなんだよと言われそうなのですが、実はマイナスの数値の折り出しは可能です。使う機会はほぼ無いのですが、一応、数字の分け方の選択肢が広くなります。
実用性はあまりないのですが、今回のような「-1」であれば使えそうです。なお、私自身もまさかこれを使うことがあるとは思っていなかった。これだから面白い。
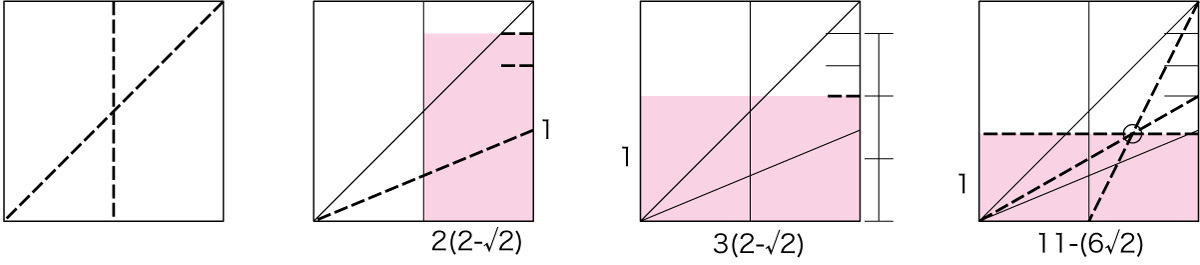
実際の手順としては、まず「2-√2」を折り出して、6等分することで「6(2-√2)」にします。
そして、マイナス方向へ対角線を伸ばして、交点を得ることで、1:11-6√2の長方形を折り出すことができます。
とりあえず手順にしてみましょう。
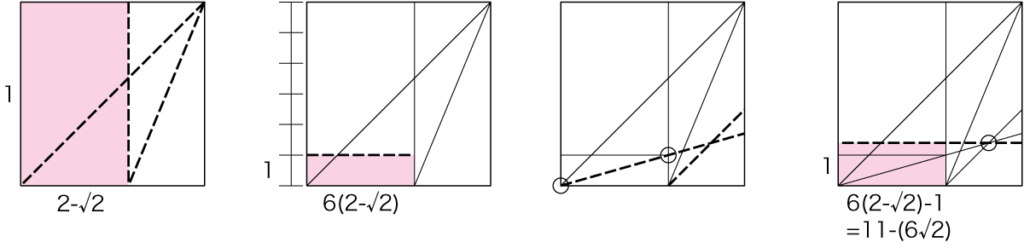
これで、なんとか必要な比率の長方形を折り出すことができました。ここから対角線を伸ばすなどして比率を折り出せます。ですが、もう少し折りやすくできないでしょうか?
マイナスの折り出しを使う場合、「折り出し点を紙の辺の中心に置いて、高さを倍にする」と、紙の1辺がそのまま折り出しの長さになります。使いやすさという点では、これを基本にするとよさそうです。
ということで、手順にするとこうなります。辺を1:11-6√2にするため、高さを倍にしています。
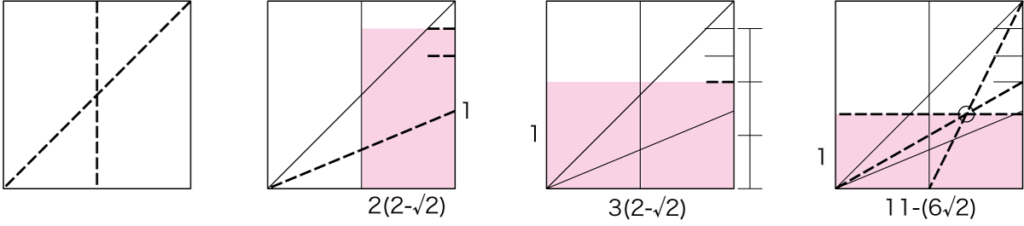
かなり折りやすくなりました。これならなんとか実用範囲です。
さて、もう一つ、普通に11と6√2を折り出すという方法も考えられます。辺を等分などして11を折り出し、反対側から6√2を折り出せば必要な比率を折り出すことができます。11を折り出すには12等分や16等分が必要ですが、実際に行う場合は必要な部分だけ切り出しで、8等分で行うのがよいでしょう。
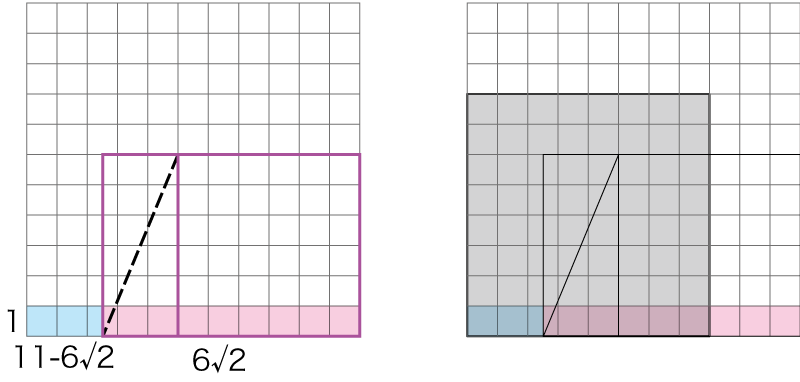
ということで実際の手順です。かなり最適化されているため、この手順だけ見せられても、そもそも何を意図しているのかを読み取るのは難しそうです。というか、分かったら割とすごい。私は即答できる自信がない。

以上、「11-6√2」の折り出し方法と、最適化についてでした。今の所、対応作品は知る限り1作品のみですが、もしこの比率が必要になった場合は自由にご利用ください。