比の折り出しスクリプトの検索候補に「4:2+√2」を追加した時に考えていたことです。
6+√2を折り出す場合、おそらく4と2+√2に分けるのがまず間違いなくベストです。どちらも数字自体は難しい比率ではないので、効率や精度を気にしなければ簡単に折り出せます。過去に4:2と2+√2:2の対角線を使っての折り出しも行なっています。ただ、2+√2:4を使うと、対角線上に折り出すことができるので、より使いやすく無駄がなさそうです。
まず、2+√2:2については、とても簡単に折り出すことができます。√2系の比率では、最も折り出しやすいものの一つでしょう。
2+√2:1はこの半分なので、こちらも折り出しは簡単です。
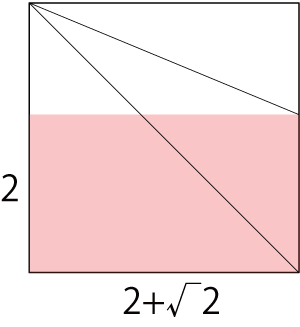
ではこの縦側の2を倍にした「2+√2:4」を使いたい場合は、どのように折り出すのがよいのでしょうか?
折り出し自体は可能なのはすぐに分かるのですが、簡単に折り出す方法があれば使いやすくなるはずです。
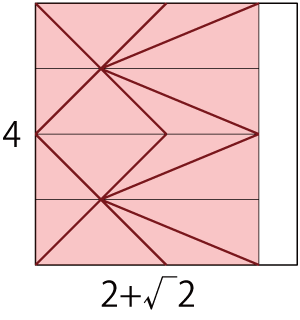
今回の基準点折り出し方法は、2+√2を3と(√2)-1に分けて考えます。
√2という数字は、(当たり前ですが)1と(√2)-1に分けることが出来ます。そして(√2)-1は、22.5度の線で簡単に折り出すことができます。
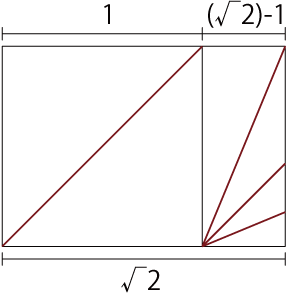
ということで、2+√2を4等分の線3マスと22.5度の線で折り出すと考えます。
1/16の小さな正方形内に22.5度の折り筋をつければ、それで基準点を折り出すことができるのです。
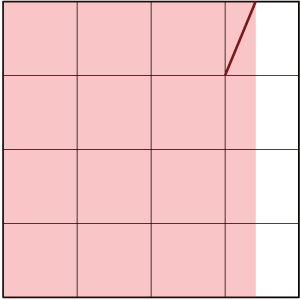
ただ、この手順だと無駄な折り筋が多いので、手順を逆にします。つまり辺を4等分してから22.5度の折り筋をつけるのではなく、先に22.5度の折り筋をつけ、それから4等分することで、ほぼ無駄な折り筋がない状態で2+√2:4の基準点を折り出す事ができました。
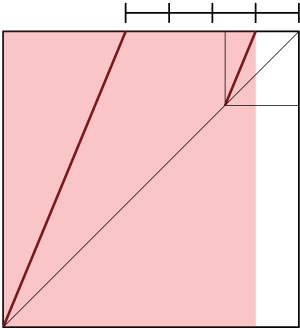
同じようにして更に半分の点にすると、8:6+√2の比率も折りだせます。
あまり実用的ではありませんが、もしかしたら使う機会があるかもしれません。
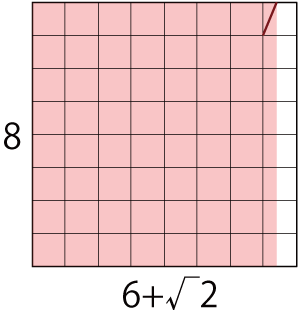
ちなみに、今回は対角線を交差させる比率折り出し方で利用していますが、もちろん他の比率の折り出し方法でも使えます。グリッドを基本としていることを考えると、むしろそっちの方で使った方が便利そう。

