2010年のメモが案外面白かったので。需要はについては考えない。

シッポ・マボナさんのアリの構造が面白い。左右の1:2の長方形にそれぞれ6つのカドが詰め込まれているという、サークルパッキングらしい、無駄の無い構造だ。 ただし、折り出しはそう簡単ではない。さて、どう折り出す？　というか、折るだけでいけるのか？

http://snkhan.co.uk/forum/viewtopic.php?t=7466

形を見ていると、なんとなく任意角の三等分を思い出すのだが、あまり関係がなさそうだ。そもそも「3等分する角度」か「3等分の起点」が分かればそれがほぼ答えだという事にすぐに気がついた。これは一旦忘れよう。

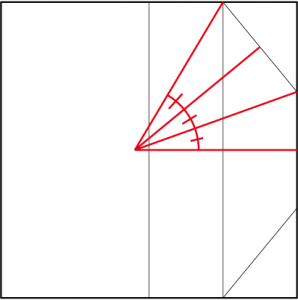
似てはいるんですけどね。

整理しよう。折り出したいのは、横の辺に位置するカドの点、もしくはカドの折り込んである線の角度だ。この場合、どちらかというと角度の方が折り出しやすそうな気がする。紙の横のカドの間隔（カドの長さを1として、この長さを2としておこう）を適当なところに折り出して、それを基準に紙の上下の点を折り出すのがよさそうだ。

で、あとはこの2の長さの円周上のどこかに上下の辺のカドがある訳だ。 なにか他にもうひとつ基準はないか……ある。

展開図で見た場合、上辺のカドと横の辺の中間点を結ぶ線は、1:2の対角線になっている。これと上記の半径2の円を組み合わせればいい訳だ。

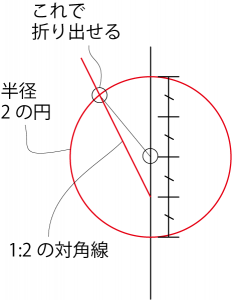
で、実際の手順。効率化してあるけれど、基本的な考え方は上記の基準を利用している。

以上。もっと良い手順があるかもしれないけど、とりあえず折り出せる事は分かったので満足。

2011/11追記。 少し後で、展開図を眺めていて、ふとまったく気がついていなかった解を見つけた。漸近法が使える！！すげえ。これ、手順がループするようなかたちで必要な点を出せば、結構応用できるんじゃないかな。

ヒダの角度を変える。ウロコ等に使えるが、使い勝手はあまりよくない。

斜めに模様を入れる構造。使い道はまだ決めていない。表側だけでなく裏側も素敵です。

10年以上前に考えた等分方法についての事と、最近の設計法が実は密接に関連していたという話。

まずは等分方法から。 切っ掛けはこの5等分。

これが何故5等分になるのかといろいろ考えていて、（なぜか）折る線が√5であることに注目、折る線の2乗等分が成立するのではないか？と思いついた。

数字を簡単に追ってみた結果、捉え方はいろいろあるにせよそれ自体は問題なさそう。ということで、やってみたのが1:4(√16)の対角線(√17)を使った17等分。

結果は成功。17等分の方法としてはかなり使いやすいのではないだろうか。

次に3等分。使うのは1:√2：√3の直角三角形、このうち折る線は√3、言い換えると1:√2の長方形の対角線になる。

√が絡むと折り出し辛いけれど、比率によっては素数等分を相当短い手順で折れる。 この段階では「ちょっと面白い等分方法で、実用面では1:√2の長方形を3等分する時に便利そう」というくらいにしか考えていなかった。

で、次が最近の話。

いわゆる神谷パターンや整数比角度系、ラングさんのsterling gridなどがいろいろと研究されているわけなのですが、先週末ごろTwitterでの話題を見ていて、上記の等分方法って実はこれらと密接に関連していたんだなと、いまさら気がついた。

この等分方法は、折ったカドの位置で縦横両方の等分が同時に出来ます。つまり、縦横等分する・カドはその等分グリッドに乗っている上に、整数の対角線ができる……他他数字から実用面までしっかり関連している。

5等分の場合、カドの位置から左側を見てみると3:4:5のいわゆる神谷パターンになる事がわかります。3等分はラングさんのsterling gridとかですね。

そして同時に気がついたのが、恐らく逆もいける。つまりこの等分方法の結果から、なんらかのグリッドが成立する。使いやすさに差はあると思うけれど、少なくとも指定の単位で折り畳める角度のセットが得られる。ベースとなる角度も比率もすぐに分かる。とりあえず整数の対角線だけはいくつか試してみたけれど、見事にピタゴラス数の構造になった。

という感じにいろいろ繋がって腑に落ちたと同時に、神谷パターンを見つけた時に感じた、「絶対他にもあるはず」という直感は当たっていたことを、とりあえず確認できたので満足したというそれだけの話。

ずいぶん前のコンベンションで宮島さんに聞かれてた問題。実は少し後に答え自体は出ていたのだけれど、放っておいて今に至る。

http://origamigasakebuyoru.seesaa.net/article/388906614.html

パターンの分析

正20面体の辺の色分けと考えるのが、個人的にはやりやすいと思う。

まず思いついたのが、それぞれの色各10枚の位置関係は対称にはならない事。正多面体の対称性を考えると、いくつかの種類に別れるはず。10の対称”面”ならあるけれど、今回はあまり使えなさそう。

次に色分け図を見て気がついたのが、5本の辺がそれぞれ繋がっている事と、それが6本絡み合っている事。これはよく考えると当たり前の話で、各頂点には5本の辺が集まっているので、3色での色分けでは必ず1:2:2となる。この1が6本の色線の端になる。で、頂点は12なので色線は6本となる。

整理されてきた。 まず、6本3色であれば対称性が分かりやすい。正四面体の各辺だ。 さらに色分け図を詳しく見ると、5本の辺はS字に曲がっている事に気がつく。たしかにこれ以外では無理っぽい。正20面体=変形正四面体であると考えれば、納得の対称性と位置関係。という事で、構造的には右巻きと左巻きの2種類がある。

※印の辺が5本繋がっている中心の辺

具体的な組み方

1. まず20面体の頂点5枚を組む。色はa(青)×1:b(赤)×2:c(緑)×2になる。

2. その周りを組んで三角形の面5つをつくる。これは自動的に決まる。使うのはa(青)×3:b(赤)×1:c(緑)×1。

3. 手順1でa(青)を使っている頂点（白印）に注目、a(青)ともう１つ(b(赤)またはc(緑))を合わせて頂点をつくる。

印の頂点を手前にする。

a(青)ともう１つ(図ではc(緑))で頂点をつくる。

4. 3つ組み合わせて三角形の面3つをつくる。

5. 2カ所あるユニットが4つ集まっている頂点のうち、片方は両側の色が違うため確定している。3つ組み合わせて面を2つつくる。

4つのユニットが集まっている印の頂点を手前に。

色はc(緑)に確定している。両側も組み合わせる。

6. あとは確定している頂点・面を順番に埋めていけば完成。

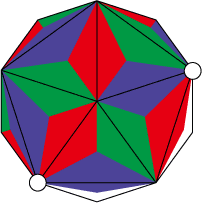印の頂点はつなぐパーツの色が確定済。それぞれ組んで進めていけば全体が組み上がる。

ポイントとなるのは3の手順で、ここで正しい色のパーツを組む事で巻き方向を確定、残りの色も全て決まります。逆にここで間違えて緑と赤を組んでしまうと、少し先で行き詰まります。線対称になっているので、2つ先くらいの手順で同じ色が隣り合うはず。

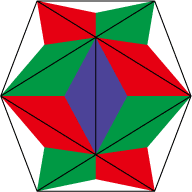これはダメなパターン。青のパーツが赤と緑で取り囲まれている。

三等分の方法と、三等分にならない方法を同時に見つけた話。

まずは以下の図をご覧下さい。1/3の折り出し方です。

ここで問題：どこが3等分になっているのでしょうか？

まずは正解から。斜めの方の点が正解で、図のように3等分しています。なお、実用性はあまり無いです。使い易くはないし、この方法を使わなければいけない必然性も思いつかない。当然、これが実際に使われている図などを私は知りません。

で、こっちはハズレ。折ってみた時はもしかしたらと思ったけれど、確認したら違った。ただ、これが妙に惜しくてちょっと面白い。

長さはピタゴラスの定理で簡単に確認できます。紙の１辺を12とすると、幅は9、高さは7.93725…..となります。15cmの紙の場合、1/3とは1mm程度の誤差です。

ちなみに、正確に3等分できる場合の三角形の面積は幅9×9+高さ8×8＝145。このケースの面積は斜辺12×12=144なので、残念ながら1ずれています。

以上、多分実用性はないけれど、方法を見つけた本人が面白かっただけの話です。

アルドゥインは、「 シンプルな形を折り出し、複雑な仕上げを行う」という方針で創られています。これは外見だけではなく、構造でも同様の方針を取っています。創作手順を簡単に追って見ていきます。

とりあえず頭部は正方形のカドから折り出すことにします。また、ツノや顎などはカドの外側にスペースを追加して折り出す方法がよさそうです。簡単な構造で必要なカドを揃える事が出来ました。

頭部とその周りの全体の構造については、頭部と翼に同じ大きさのカドを割り当てられそうです。つまり鶴の基本形でOK。中心のカドも、胴のトゲ等に利用できそうです。

全体の構造はいくつか候補が考えられますが、とりあえず最もシンプルなものを採用します。

……あまりにも普通の構造で、これでいいのかと思うかもしれませんが、カドの出る位置は悪くないし、わざわざ必要以上に複雑にする意味はありません。昔『をる』誌上で前川さんも言っていましたが、構造がシンプルなのは歓迎すべき事で、わざわざ複雑にしなければいけないのではと気にするのはおかしい。

※領域の追加を前提とした場合、基礎の構造を選ぶ時には、カドの大きさより出ている位置を優先します。カドの大きさは領域の追加でいくらでも調整可能です。

これを基礎として、必要に応じて領域を追加していきます。ここはいろいろな要素が絡むので結果から。

一気に説明します。基礎構造（白）に、まずは頭部の折り出し用の領域を追加（赤）。 足の指と尾の装飾用に反対側にも追加（黄）。そして翼が少し小さいので、中心をぶった切ってさらに領域を追加します（青）。なおこの部分は、脚の装飾や翼の爪の折り出しにも利用しています。

※気がついた方もいるかもしれませんが、この3回の領域の追加は、すべて同じ幅になっています。このおかげて翼の爪部分をきれいに折り出す事が出来ます。また、比率も分かりやすくなります。

これで十分なカドは出そろいました。あとは仕上げればできあがりです。

22.5度の原子で遊んでいると、折り出しにくい比率が必要になる時があります。という事で、最もよく出現するものの一つ、3+√2という比率について。

まず。とりあえず以下のような構造が3+√2です。

左はビバ！おりがみに掲載されている前川淳さんの龍、中央は川畑文昭さんのディノニクスなどが有名でしょうか。

※余談ですが、この2つの作品はどちらも大好きな作品で、よく折っていたのですが、自分で創作を始めるまで、これらが同じ比率を使っていた事に気がつきませんでした。

折り出しの点はいくつか考えられますが、2:1+√2、もしくは1:2+√2に分けるのが使いやすいでしょう。

※3:√2も出来ますが、折り出しやすさを考えるとあまりメリットはないように思います。

まずは、ビバ！の龍の折り出して紹介されたものです。対角線上に折り出されるので使いやすいですね。

もう一つ、折り出されるのは上記の方法と同じ点になります。（少し折り筋の付け方は違いますが、川畑さんの恐竜で使われている方法です。）

2つとは違い1:2+√2に分割する方法です。これも対角線に折り出されます。欲しい点に合わせて使い分けるとよいでしょう。

ブック型の対称線に折り出す方法です。
構造によってはこちらの方が使いやすい場合もあります。

実際に折っている時には当たり前で意識していないような事でも、整理しておくと意味があるかもしれない。

ということで、幅変換の話。一般的に蛇腹のテクニックというイメージがあるけれど、直角以外でも結構普通に使える。そして、実は平行のヒダ同士でなくても使える。

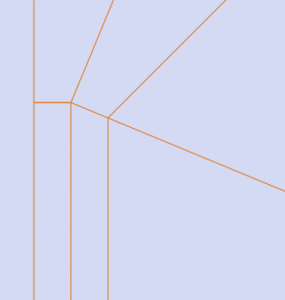
ヒダを細くするとこうなる。中心に現れる22.5度の直角三角形が面白い。もちろん、もっと細かくしても折れるはず。

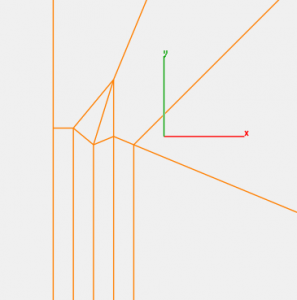
平行じゃない方でもいけます。

ここまでくれば予想は出来ると思うけれど、当然両側が平行でない場合でも可能。

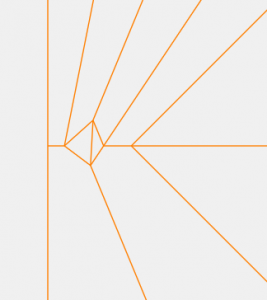
この辺になると、幅変換と意識されていないのではないだろうか。ただ本質的には同じ仕組みのはず。後は、ラインが一値ではないしずめ折りや、いわゆるSpread-sinkをして折り畳んだ形が同じ構造になります。

以上、細かい検証とかは好きな方にお任せします。