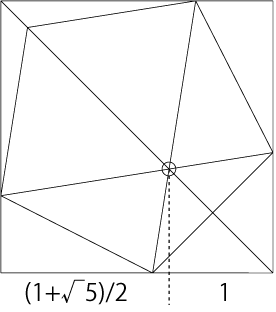
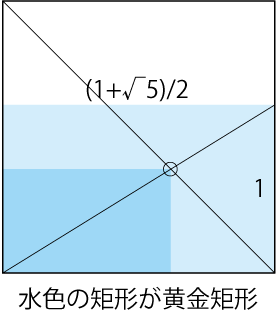
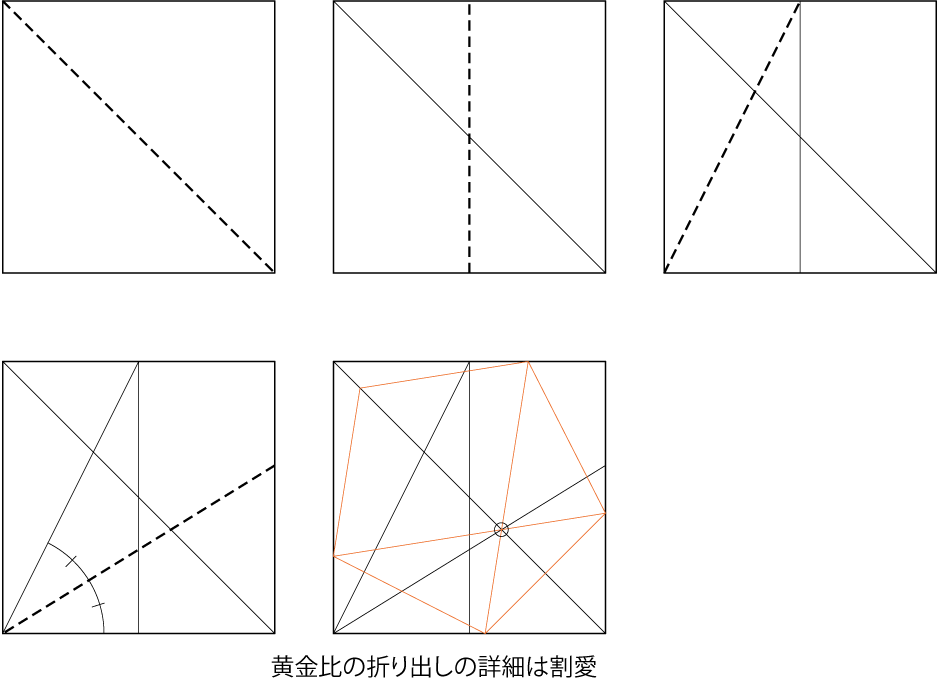
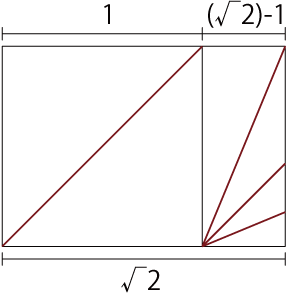
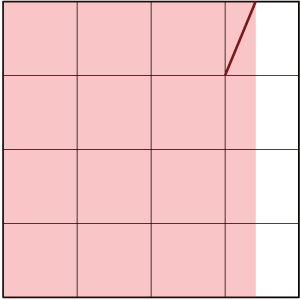
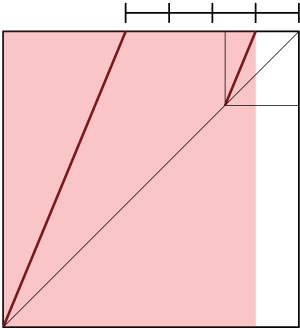
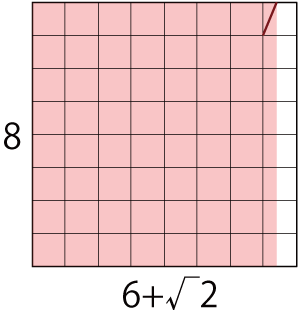
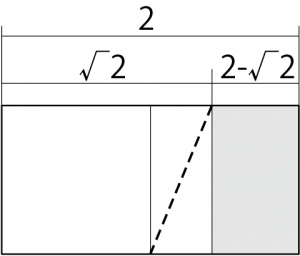
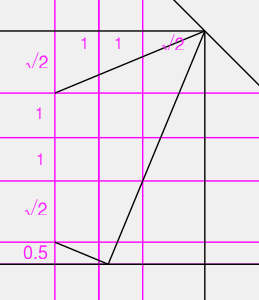
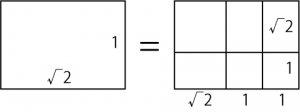
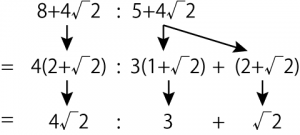元ツイートは「光あれ」のパロディなのですが、せっかくなので。
自分の覚えている範囲だと、『おりがみ新世紀』に掲載されているジョン・モントロール氏のサメには、折り筋で表現されたエラがありました。また『Origami Sea Life』のサメでも、段折りでエラの表現がされています。
余談ですが、モントロール氏は、一定の範囲の技術(=折り図にできるもので、折り紙に慣れていないアメリカ人がなんとか折れるかもと思える範囲)で、様々な題材の作品を創作されています。折るべき形や、要素の取捨選択が優れた作家であると言えるかもしれません。
ラブカなどを含めると他にも作例はありそうだし、冗談ではなく「吉澤さんが50年前にやってる」でもおかしくありません。(覚えている限りでは、吉澤章氏のサメの折り図はなかったと思うのですが、折り図になっていないしっかりエラが折り出された作品があっても不思議ではありません。)
ちなみに私がエラを折り出したのは、自作のエイや吉野氏のマンタなどで、エラは割と効果的なのを知っていたのと、歯よりも低コストで実装できそうだったからです。要するに歯を割愛する代わりにつけた。
ヒダを構造に組み込むと難しくなるけれど、外側にカドを出して段折りであればわりと簡単に実装できること、またサメの特等的なパーツであることが知られたので、最近の作品でエラつきが増えたということなのでしょう。